Таблица 1. Результаты теста - прыжок в длину с разбега - мальчики, мужчины

Таблица 1

Примечание: РМ - рекорды мира; ЗД - здоровые, Гл - с поражением слуха, ЛИН - лица с интеллектуальными нарушениями, В1, В2, В3 - незрячие спортсмены. Индексом "ю" помечены юношеские разряды.

2. На рис. 7 - 9 демонстрируются графики, отображающие рекорд мира и зависимость уровня спортивного мастерства мальчиков и мужчин (результаты в прыжке в длину с разбега) от спортивной категории (спортивного звания и спортивного разряда) спортсменов-олимпийцев, паралимпийцев (с нарушением зрения и интеллекта) и сурдлимпийцев (с нарушением слуха). Для наглядности на рис. 7 даны графики здоровых спортсменов и спортсменов с нарушением зрения (В1, В2, В3), на рис. 8 - здоровых спортсменов и спортсменов с нарушением слуха (Гл) и на рис. 9 - здоровых и лиц с интеллектуальными нарушениями (ЛИН).

Предварительный анализ данных табл. 1 и графиков на рис. 7 - 9. позволяет сделать предположение, что эти данные ложатся на довольно гладкую кривую с большими радиусом кривизны, почти прямую.

Чтобы учесть эффекты вариативности данных и найти объективную шкалу для исследования зависимостей и поиска тенденций, были применены стандартные математико-статистические приемы исследования небольших выборок данных.

В том числе, сделан расчет математического ожидания, стандартного отклонения, вычислены доверительные интервалы для различной вероятности отклонения от принятой гипотезы. Было определено, что использование t-распределения Стьюдента даст более достоверные результаты для аппроксимирующих кривых по сравнению с использованием нормального распределения.

Результаты аппроксимации зависимостей спортивного мастерства от спортивной квалификации с помощью линейной и экспоненциальной аппроксимации рядов данных подтверждают попадание значения аппроксимирующей функции в доверительный интервал 0,05. При подборе более сложной полиномиальной аппроксимирующей функции был получен еще более точный результат. Аппроксимация такого типа может использоваться для определения искомых корректировочных коэффициентов.

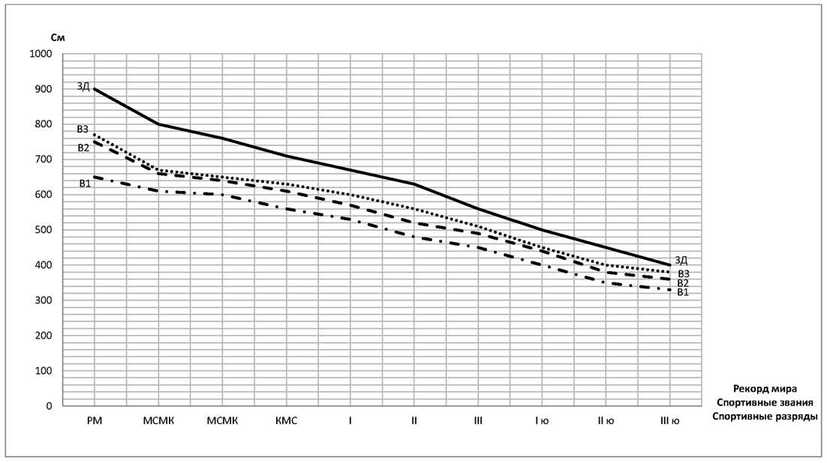
Рис. 7 Результаты рекорда мира (РМ) спортивных званий (МСКМ, МС), спортивных разрядов (КМС, I, II, III, I ю, II ю, III ю) здоровых и слепых мальчиков и мужчин в тесте - прыжок в длину с разбега.

Рис. 8. Результаты рекорда мира (РМ) спортивных званий (МСКМ, МС), спортивных разрядов (КМС, I, II, III, I ю, II ю, III ю) здоровых и глухих мальчиков и мужчин в тесте - прыжок в длину с разбега.

Рис. 9. Результаты рекорда мира (РМ) спортивных званий (МСКМ, МС), спортивных разрядов (КМС, I, II, III, I ю, II ю, III ю) у мальчиков и мужчин (здоровых и с интеллектуальными нарушениями) в тесте - прыжок в длину с разбега.

3. С целью поиска более объективной шкалы, необходимой для построения "функциональной зависимости уровня спортивного мастерства от категории спортсменов", используем принятый в экспериментальной физике метрологический подход к построению так называемых разностных шкал. Для таких шкал отсчеты берутся в виде разницы между заранее известным предельным значением шкалы и точкой измерения. В нашем случае в качестве предельного значения шкалы берется показатель рекорда мира, а промежуточными точками выступают нормы спортивных званий и спортивных разрядов [9].

Нелинейная разностная шкала (РМ - норма конкретного спортивного звания, спортивного разряда) представлена в табл. 2 для здоровых мальчиков и мужчин и инвалидов мужского пола различных нозологических групп. Она построена на основе действующей ЕВСК (2014 - 2017 гг.) и позволяет выявить тенденции в падении значения функции уровня мастерства по мере удаления от рекорда мира для различных категорий (званий, разрядов) спортсменов.