Если случайные переменные xi статистически независимы, то доверительный интервал функции ![]() связан с доверительными интервалами переменных
связан с доверительными интервалами переменных ![]() соотношением (доверительные интервалы берутся для одной и той же вероятности):
соотношением (доверительные интервалы берутся для одной и той же вероятности):
Данное выражение является обобщением соотношения (5.2).
При испытании лекарственных средств методами физического, физико-химического и химического методами анализа измеряемая величина y представляет собой обычно произведение или частное случайных и постоянных величин (масс навесок, разведений, поглощений или площадей пиков и т.д.), т.е. (К - некая константа):
В этом случае соотношение (4.2) принимает вид:
где использованы относительные доверительные интервалы.
Соотношение (5.4) применимо при любых (разных) степенях свободы (в том числе и бесконечных) для величин xi. Его преимуществом является простота и наглядность. Использование абсолютных доверительных интервалов приводит к гораздо более громоздким выражениям, поэтому рекомендуется использовать относительные величины.
При проведении испытаний лекарственных средств в суммарной неопределенности 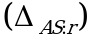 анализа обычно всегда можно выделить такие типы неопределенностей: неопределенность пробоподготовки
анализа обычно всегда можно выделить такие типы неопределенностей: неопределенность пробоподготовки 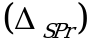 , неопределенность конечной аналитической операции
, неопределенность конечной аналитической операции 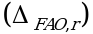 и неопределенность аттестации стандартного образца
и неопределенность аттестации стандартного образца 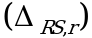 . Величина
. Величина ![]() обычно мала, поэтому в приведенном выражении она не использована. Учитывая это, а также то, что анализ проводится и для испытуемого раствора (индекс "smp"), и для раствора сравнения (индекс "st"), выражение (5.5) можно представить в виде:
обычно мала, поэтому в приведенном выражении она не использована. Учитывая это, а также то, что анализ проводится и для испытуемого раствора (индекс "smp"), и для раствора сравнения (индекс "st"), выражение (5.5) можно представить в виде:
При этом каждое из слагаемых рассчитывают из входящих в него компонентов по уравнению (5.5).
Если число степеней свободы величин xi одинаково или достаточно велико (> 30), выражение (5.5) дает:
Это же соотношение получают при тех же условиях и из выражения (5.2).
- Гражданский кодекс (ГК РФ)
- Жилищный кодекс (ЖК РФ)
- Налоговый кодекс (НК РФ)
- Трудовой кодекс (ТК РФ)
- Уголовный кодекс (УК РФ)
- Бюджетный кодекс (БК РФ)
- Арбитражный процессуальный кодекс
- Конституция РФ
- Земельный кодекс (ЗК РФ)
- Лесной кодекс (ЛК РФ)
- Семейный кодекс (СК РФ)
- Уголовно-исполнительный кодекс
- Уголовно-процессуальный кодекс
- Производственный календарь на 2025 год
- МРОТ 2026
- ФЗ «О банкротстве»
- О защите прав потребителей (ЗОЗПП)
- Об исполнительном производстве
- О персональных данных
- О налогах на имущество физических лиц
- О средствах массовой информации
- Производственный календарь на 2026 год
- Федеральный закон "О полиции" N 3-ФЗ
- Расходы организации ПБУ 10/99
- Минимальный размер оплаты труда (МРОТ)
- Календарь бухгалтера на 2026 год
- Частичная мобилизация: обзор новостей
- Постановление Правительства РФ N 1875
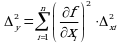 . (5.3)
. (5.3)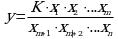 . (5.4)
. (5.4)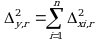 , (5.5)
, (5.5)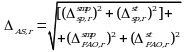 . (5.6)
. (5.6)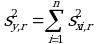 , (5.7)
, (5.7)